Derive: tQ Model -- Enzyme Kinetics
derive_tQ_model.RmdEnzyme Kinetic Modeling
Enzymes are proteins that catalyze chemical reactions. Not only do they facilitate producing virtual all biological matter, but they are crucial for regulating biological processes. In the early 20th century Michaelis and Menten described a foundational kinematic model for enzymes, where the substrate and enzyme reversibly bind, the substrate is converted to the product and then released.
kf
---> kcat
E + S <--- C ---> E + P
kbwhere the free enzyme (E) reversibly binds to the stubstrate (S) to
form a complex (C) with forward and backward rate constants of kf and
kb, which is irreversibly catalyzed into the product (P), with rate
constant of kcat, releasing the enzyme to catalyze additional substrate.
The total enzyme concentration is defined to be the
ET := E + C. The total substrate and product concentration
is defined to be ST := S + C + P. The Michaelis constant is
the defined to be the kM := (kb + kcat) / kf. The
kcat rate constant determines the maximum turn over at
saturating substrate concentrations, Vmax := kcat * ET. The
rate constants kcat and kM can be estimated by
monitoring the product accumulation over time (enzyme progress curves),
by varying the enzyme and substrate concentrations.
By assuming that the enzyme concentration is very low (ET <<
ST), they derived their celebrated Michaelis-Menten kinetics. Since
their work, a number of groups have developed models for enzyme kinetics
that make less stringent assumptions. Recently (Choi, et al., 2017),
described a Bayesian model for the total QSSA model. To make their model
more accessible, we have re-implemented it in the Stan/BRMS framework
and made it available through the BayesPharma package.
Outline for Vignette
Next we will formally define the problem and formulate the model as
the solution to an ordinary differential equation. To illustrate, we
will consider a a toy system where we assuming the kcat and
kM are known and simulate a sequence of measurements using
deSolve. We will then implement the ODE in Stan/BRMS using stanvars and
show how the parameters of the toy system can be estimated. Since it is
common to vary the enzyme and substrate concentrations in order to
better estimate the kinematic parameters, we will show how we can
improve the Stan/BRMS model to allow multiple observations, each with an
arbitrary number of measurements. Then finally, we will consider a real
enzyme kinetics data set and use the Stan/BRMS model to estimate the
kinematic parameters. We will compare estimated parameters with those
fit using standard approaches.
Problem Statement
Implement the total QSSA model in stan/BRMS, a refinement of the classical Michaelis-Menten enzyme kinetics ordinary differential equation described in (Choi, et al., 2017, DOI: 10.1038/s41598-017-17072-z). From their equation 2:
Observed data:
M = number of measurements # The product concentration Pt is measured
t[M] = time # at M time points t
Pt[M] = product #
ST = substrate total conc. # Substrate and enzyme concentrations are
ET = enzyme total conc. # assumed to be given for each observation
Model parameters:
kcat # catalytic constant
kM # Michaelis constant
ODE formulation:
dPdt = kcat * ( # Change in product concentration at time t
ET + kM + ST - Pt +
-sqrt((ET + kM + ST - Pt)^2 - 2* ET * (ST - Pt))) / 2
initial condition:
P := 0 # There is zero product at time 0In (Choi, et al. 2017) they prove, that the tQ model is valid when
K/(2*ST) * (ET+kM+ST) / sqrt((ET+kM+ST+P)^2 - 4*ET(ST-P)) << 1,where K = kb/kf is the dissociation constant.
Simulate one observation
Using the deSolve package we can simulate data following
the total QSSA model. Measurements are made with random Gaussian noise
with mean 0 and variance of 0.5.
tQ_model_generate <- function(time, kcat, kM, ET, ST){
ode_tQ <- function(time, Pt, theta){
list(c(theta[1] * (
ET + theta[2] + ST - Pt +
-sqrt((ET + theta[2] + ST - Pt)^2 - 4 * ET * (ST - Pt))) / 2))
}
deSolve::ode(y = 0, times = time, func = ode_tQ, parms = c(kcat, kM))
}
data_single <- tQ_model_generate(
time = seq(0.00, 3, by=.05),
kcat = 3,
kM = 5,
ET = 10,
ST = 10) |>
as.data.frame() |>
dplyr::rename(P_true = 2) |>
dplyr::mutate(
P = rnorm(dplyr::n(), P_true, 0.5), # add some observational noise
ST = 10, ET = 10)
head(data_single)## time P_true P ST ET
## 1 0.00 0.0000000 -0.08982865 10 10
## 2 0.05 0.7311578 1.34853281 10 10
## 3 0.10 1.4243598 1.43308014 10 10
## 4 0.15 2.0794197 1.73661838 10 10
## 5 0.20 2.6964485 2.78619356 10 10
## 6 0.25 3.2758537 3.17795634 10 10To visualize, the true enzyme progress curve is shown in blue, and the enzyme progress curve fit to the
noisy measurements with a smooth loess spline is shown in
orange. While the smooth fits well, we
cannot estimate the parameters for the curve from it.
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was generated.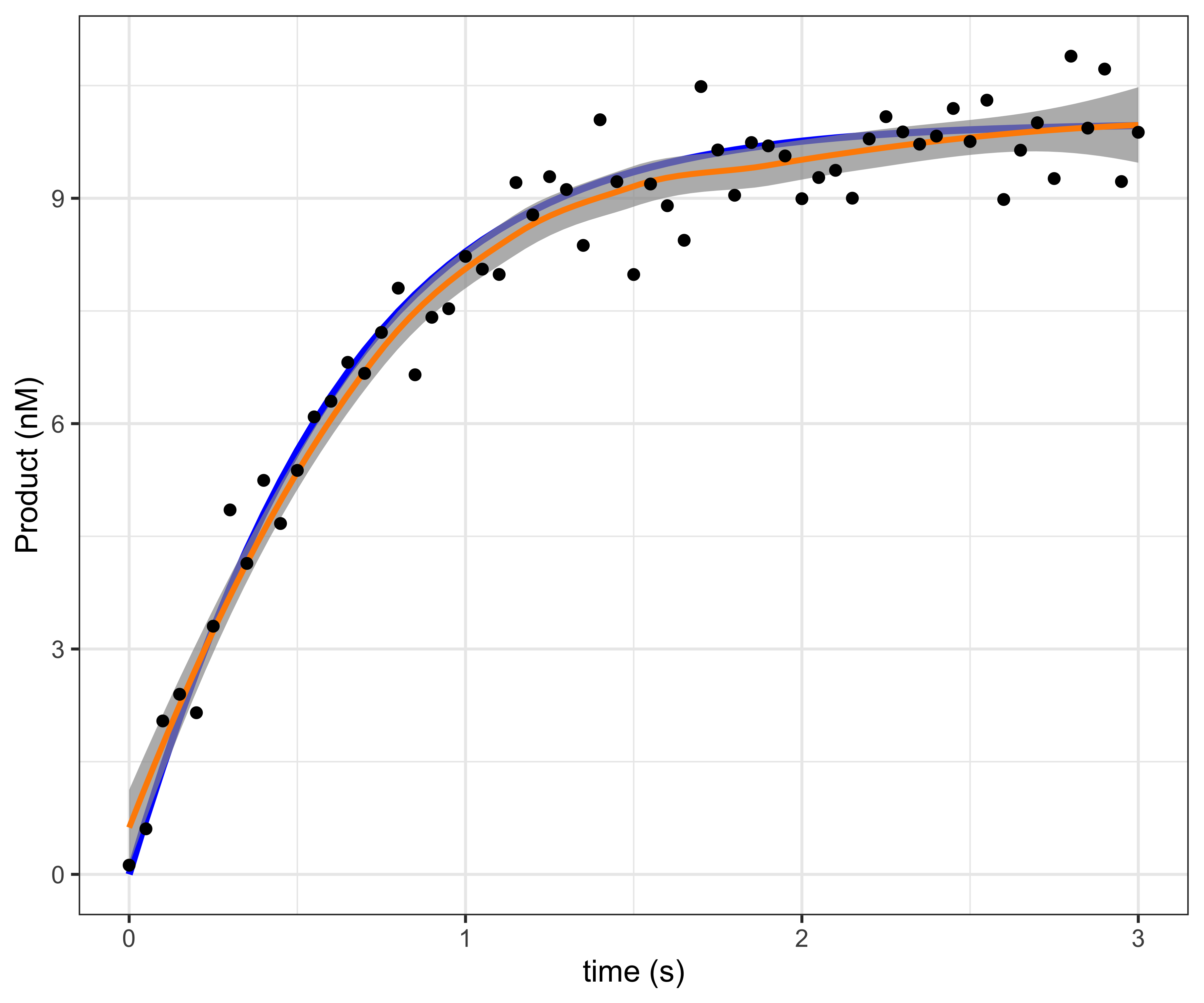
plot of chunk data-single-plot
Fitting a single ODE observation in BRMS
To implement in BRMS, we can use the stanvars to define
custom functions. The key idea is call the ODE solver, in this case the
backward differentiation formula (bdf) used to solve stiff ODEs, passing
a function ode_tQ that returns dP/dt, the
change in product at time t. The ode_tQ
function depends on the product at time t as the state
vector, the kinematic parameters to be estimated kcat and
kM and the user-provided data of the enzyme and substrate
concentrations ET and ST. To call
ode_dbf we pass in the initial product concentration and
time (both equal to zero), measured time-points, parameters and user
defied data. Finally we, extract the vector of sampled vector of product
concentrations which we return.
stanvars_tQ_ode <- brms::stanvar(scode = paste("
vector tQ_ode(
real time,
vector state,
vector params,
data real ET,
data real ST) {
real Pt = state[1]; // product at time t
real kcat = params[1];
real kM = params[2];
vector[1] dPdt;
dPdt[1] = kcat * (
ET + kM + ST - Pt
-sqrt((ET + kM + ST - Pt)^2 - 4 * ET * (ST - Pt))) / 2;
return(dPdt);
}
", sep = "\n"),
block = "functions")
stanvars_tQ_single <- brms::stanvar(scode = paste("
vector tQ_single(
data vector time,
vector vkcat,
vector vkM,
data vector vET,
data vector vST) {
vector[2] params = [ vkcat[1], vkM[1] ]';
vector[1] initial_state = [ 0.0 ]';
real initial_time = 0.0;
int M = dims(time)[1];
vector[1] P_ode[M] = ode_bdf( // Function signature:
tQ_ode, // function ode
initial_state, // vector initial_state
initial_time, // real initial_time
to_array_1d(time), // array[] real time
params, // vector params
vET[1], // ...
vST[1]); // ...
vector[M] P; // Need to return a vector not array
for(i in 1:M) P[i] = P_ode[i,1];
return(P);
}
", sep = "\n"),
block = "functions")To use this function, we define kcat and kM
as parameters and that we wish to sample P ~ tQ(...). Since
all the data points define a single observation, we set
loop = FALSE. We use gamma priors for
kcat and kM with the shape parameter
alpha=4 and the rate parameter beta=1. The
prior mean is alpha/beta = 4/1 = 4 and the variance is
alpha/beta^2 = 4/1 = 4. We also bound the parameters from
below by 0. We initialize each chain at the prior mean and
use cmdstanr version 2.29.2 as the backend, and use the
default warmup of 1000
brms_params <- list(
cores = 4,
seed = 52L,
backend = 'cmdstanr')
model_single <- do.call(what = brms::brm, args = c(list(
formula = brms::brmsformula(
P ~ tQ_single(time, kcat, kM, ET, ST),
kcat + kM ~ 1,
nl = TRUE,
loop=FALSE),
data = data_single |> dplyr::filter(time > 0),
prior = c(
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kcat"),
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kM")),
init = function() list(kcat = 4, kM = 4),
stanvars = c(
stanvars_tQ_ode,
stanvars_tQ_single)),
brms_params))## Syntax error in '/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-14253748bb373.stan', line 34, column 18 to column 19, parsing error:
## -------------------------------------------------
## 32: int M = dims(time)[1];
## 33:
## 34: vector[1] P_ode[M] = ode_bdf( // Function signature:
## ^
## 35: tQ_ode, // function ode
## 36: initial_state, // vector initial_state
## -------------------------------------------------
##
## ";" expected after variable declaration.
## It looks like you are trying to use the old array syntax.
## Please use the new syntax:
## array[M] vector[1] P_ode;## make[1]: *** [/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-14253748bb373.hpp] Error 1## Error: An error occured during compilation! See the message above for more information.Fitting the model takes ~15 seconds, with Rhat = 1 and
effective sample size for the bulk and tail greater than
1400 for both parameters. The estimates and 95% confidence
intervals are good.
## Error in eval(expr, envir, enclos): object 'model_single' not foundTo visualize the posterior distribution vs. the prior distribution,
we first sample from the prior, using the same brms::brm
call with sample_prior = "only" the argument.
model_single_prior <- do.call(what = brms::brm, args = c(list(
formula = brms::brmsformula(
P ~ tQ_single(time, kcat, kM, ET, ST),
kcat + kM ~ 1,
nl = TRUE,
loop=FALSE),
data = data_single |> dplyr::filter(time > 0),
prior = c(
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kcat"),
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kM")),
init = function() list(kcat = 4, kM = 4),
stanvars = c(
stanvars_tQ_ode,
stanvars_tQ_single),
sample_prior = "only"),
brms_params))## Syntax error in '/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-142534112e1ed.stan', line 34, column 18 to column 19, parsing error:
## -------------------------------------------------
## 32: int M = dims(time)[1];
## 33:
## 34: vector[1] P_ode[M] = ode_bdf( // Function signature:
## ^
## 35: tQ_ode, // function ode
## 36: initial_state, // vector initial_state
## -------------------------------------------------
##
## ";" expected after variable declaration.
## It looks like you are trying to use the old array syntax.
## Please use the new syntax:
## array[M] vector[1] P_ode;## make[1]: *** [/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-142534112e1ed.hpp] Error 1## Error: An error occured during compilation! See the message above for more information.And to plot, we use tidybayes to gather the draws and
ggplot2 to map them to curves, with the prior as theorange curve, posterior as the blue curve, and the true parameter marked as a
vertical line.
## Error in eval(expr, envir, enclos): object 'model_single_prior' not found## Error in eval(expr, envir, enclos): object 'model_single' not found## Error in eval(expr, envir, enclos): object 'draws_single_prior' not foundNext, we plot the prior and posterior samples as a scatter plot. Note
that the high correlation of the kcat and kM
parameters in the posterior. This is expected, and typically better
estimates require varying the enzyme and substrate concentrations.
## Error in eval(expr, envir, enclos): object 'draws_single_prior' not found## Error in eval(expr, envir, enclos): object 'draws_single_posterior' not found## Error in eval(expr, envir, enclos): object 'draws_single_prior_pairs' not foundFitting multiple observations
Next we will extend the BRMS model to allow fitting common
kcat, kM concentrations based on multiple
replicas, or varying substrate/enzyme concentrations using BRMS. To
demonstrate, we varying the enzyme and substrate concentrations, to
better fit the kinematic parameters.
data_multiple <- tidyr::expand_grid(
kcat = 3,
kM = 5,
ET = c(3, 10, 30),
ST = c(3, 10, 30)) |>
dplyr::mutate(observation_index = dplyr::row_number()) |>
dplyr::rowwise() |>
dplyr::do({
data <- .
time <- seq(0.05, 3, by=.05)
data <- data.frame(data,
time = time,
P = tQ_model_generate(
time = time,
kcat = data$kcat,
kM = data$kM,
ET = data$ET,
ST = data$ST)[,2])
}) |>
dplyr::mutate(
P = rnorm(dplyr::n(), P, 0.5))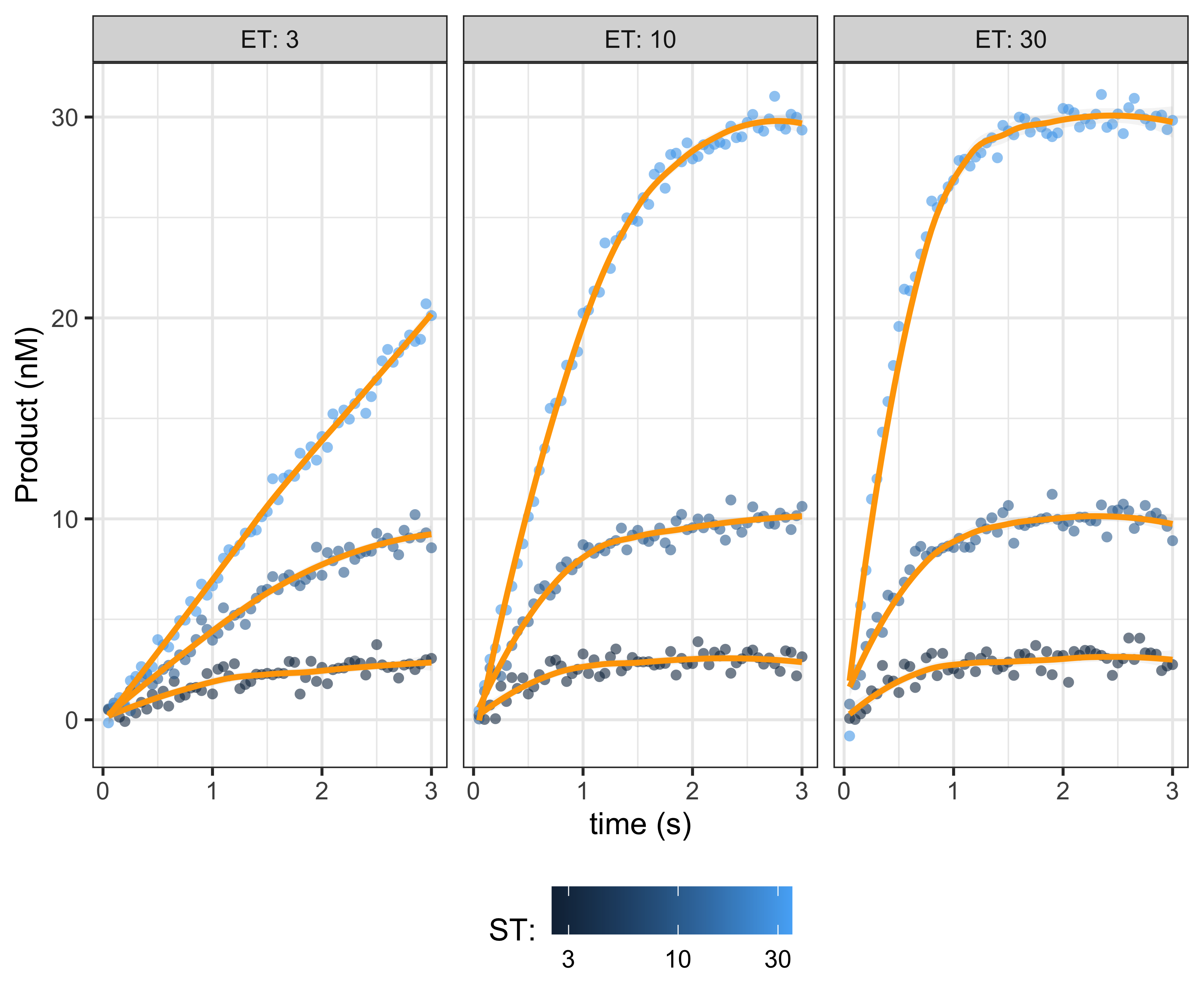
plot of chunk data-multiple-plot
stanvars_tQ_multiple <- brms::stanvar(scode = paste("
vector tQ_multiple(
array[] int replica,
data vector time,
vector vkcat,
vector vkM,
data vector vET,
data vector vST) {
int N = size(time);
vector[N] P;
int begin = 1;
int current_replica = replica[1];
for (i in 1:N){
if(current_replica != replica[i]){
P[begin:i-1] = tQ_single(
time[begin:i-1],
vkcat,
vkM,
vET[begin:i-1],
vST[begin:i-1]);
begin = i;
current_replica = replica[i];
}
}
P[begin:N] = tQ_single(time[begin:N], vkcat, vkM, vET[begin:N], vST[begin:N]);
return(P);
}", sep = "\n"),
block = "functions")
model_multiple <- do.call(what = brms::brm, args = c(list(
formula = brms::brmsformula(
P ~ tQ_multiple(observation_index, time, kcat, kM, ET, ST),
kcat + kM ~ 1,
nl = TRUE,
loop=FALSE),
data = data_multiple,
prior = c(
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kcat"),
brms::prior(prior = gamma(4, 1), lb = 0, nlpar = "kM")),
init = function() list(kcat = 4, kM = 4),
stanvars = c(
stanvars_tQ_ode,
stanvars_tQ_single,
stanvars_tQ_multiple)),
brms_params))## Syntax error in '/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-142532f07ca55.stan', line 34, column 18 to column 19, parsing error:
## -------------------------------------------------
## 32: int M = dims(time)[1];
## 33:
## 34: vector[1] P_ode[M] = ode_bdf( // Function signature:
## ^
## 35: tQ_ode, // function ode
## 36: initial_state, // vector initial_state
## -------------------------------------------------
##
## ";" expected after variable declaration.
## It looks like you are trying to use the old array syntax.
## Please use the new syntax:
## array[M] vector[1] P_ode;## make[1]: *** [/var/folders/7z/yfz7cw1d0gs8lf1mzdgkv1pw0000gn/T/RtmpsyOm66/model-142532f07ca55.hpp] Error 1## Error: An error occured during compilation! See the message above for more information.
model_multiple## Error in eval(expr, envir, enclos): object 'model_multiple' not found## Error in eval(expr, envir, enclos): object 'model_multiple' not found## Error in eval(expr, envir, enclos): object 'model_multiple_prior' not found## Error in eval(expr, envir, enclos): object 'model_multiple' not found## Error in eval(expr, envir, enclos): object 'draws_multiple_prior' not found## Error in eval(expr, envir, enclos): object 'draws_multiple_posterior' not found## Error in eval(expr, envir, enclos): object 'draws_multiple_prior_pairs' not foundNext we will sample enzyme progress curves from the posterior
## Error in eval(expr, envir, enclos): object 'draws_multiple_posterior' not found## Error in eval(expr, envir, enclos): object 'sample_multiple' not found