Apply: Sigmoid Model -- KOR Antagonists
Analysis of Four Kappa Opioid Receptor Antagonists
apply_sigmoid_KOR.RmdHill Equation
In this case study, we are going to reanalyze the dose responses of 4
Kappa Opioid receptor (KOR) antagonists from a study performed by
Margolis et al. (-@Margolis2020-bm) using
the BayesPharma package. Whole cell electrophysiology in
acute rat midbrain slices was used to evaluate the pharmacological
properties of four novel KOR antagonists: BTRX-335140, BTRX-395750,
PF-04455242, and JNJ-67953964.
Originally, the dose-response analysis was performed using the
drc package in R, which implements the minimization of
negative log likelihood function and reduces to least square estimation
for a continuous response. The data were normalized to % baseline
agonist response, measuring the extent of blockade of agonist response
in the presence of different concentrations of antagonist. These data
were then fit to a 4-parameter log-logistic dose response model, setting
the top (max agonist response) to 100% and estimating the IC50, its
variance, and the bottom (min agonist response).
Fitting the sigmoid model
Using the BayesPharma package, we can re-fit the sigmoid
model with a negative slope, and fix the top parameter to
100 as the response is normalized to a no-antagonist
baseline.
For the prior, we are going to use a normal distribution because the
response values are continuous. First, we will run the analysis with the
top (max response) parameter prior set to a constant value
of 100 because top is normalized to
100 and is the default broad prior for the
ic50, hill, and bottom
parameters. Broad priors represent unbiased uncertainty and provide an
opportunity for extreme responses.
The level of informativeness of the prior will affect how much influence the prior has on the model. Here is more information on prior choice recommendations.
kor_prior <- BayesPharma::sigmoid_antagonist_prior(top = 100)
kor_prior
## prior class coef group resp dpar nlpar lb ub source
## normal(-6, 2.5) b ic50 <NA> <NA> user
## normal(-1, 1) b hill <NA> 0.01 user
## constant(100) b top <NA> <NA> user
## normal(0, 0.5) b bottom <NA> <NA> userPrior predictive checks
Following the Bayesian workflow, before fitting the model, it is good
to check the prior predictive distributions to see if they are
compatible with the domain expertise. So, before running the model, we
will verify that the prior distributions cover a plausible range of
values for each parameter. To do this, we want to sample only from the
prior distributions by adding sample_prior = "only" as an
argument to the sigmoid_model function. We will use the
default response distribution of the model
(family = gaussian()).
kor_sample_prior <- BayesPharma::sigmoid_model(
data = kor_antag |> dplyr::select(substance_id, log_dose, response),
formula = BayesPharma::sigmoid_antagonist_formula(),
prior = kor_prior,
init = BayesPharma::sigmoid_antagonist_init(),
sample_prior = "only")And then plot of the prior predictive distributions:
kor_sample_prior |>
BayesPharma::plot_density_distribution()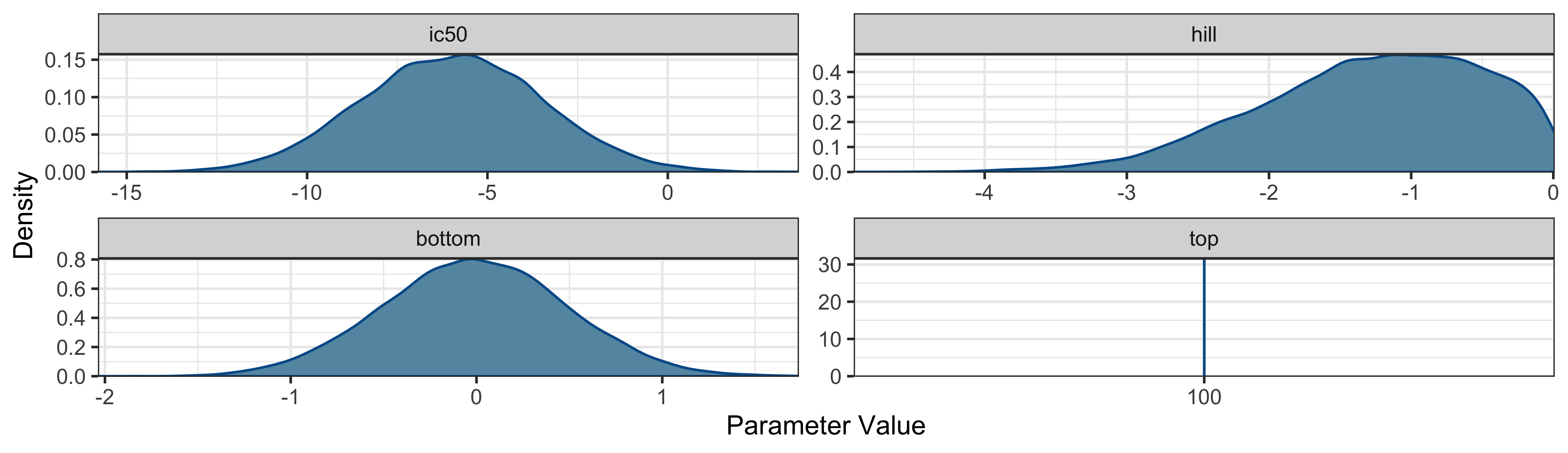
KOR antagonists prior distribution
To sample from the model, we will use the Stan NUTs
Hamiltonian Monte Carlo, and initialize the parameters to the prior
means to help with model convergence, using the default values of
ec50 = -9, hill = -1, top = 100,
bottom = 0.
kor_model <- BayesPharma::sigmoid_model(
data = kor_antag |> dplyr::select(substance_id, log_dose, response),
formula = BayesPharma::sigmoid_antagonist_formula(
predictors = 0 + substance_id),
prior = kor_prior,
init = BayesPharma::sigmoid_antagonist_init())Analyzing model fit
The brms generated model summary shows the formula that
the expected response a is sigmoid function of the log_dose
with four parameters, and a shared Gaussian distribution. Each parameter
is dependent on the substance_id. Since we want to fit a
separate model for each substance, we include a 0 + to
indicate that there is no common intercept. The data consists of
73 data points and the posterior sampling was done in
4 chains each with 8000 steps with
4000 steps of warm-up. The population effects for each
parameter summarize the marginal posterior distributions, as well as the
effective sample size in the bulk and tail. This gives an indication of
the sampling quality, with an ESS of > 500 samples being
good for this type of model.
## Family: gaussian
## Links: mu = identity; sigma = identity
## Formula: response ~ sigmoid(ic50, hill, top, bottom, log_dose)
## ic50 ~ 0 + substance_id
## hill ~ 0 + substance_id
## top ~ 0 + substance_id
## bottom ~ 0 + substance_id
## Data: data (Number of observations: 73)
## Draws: 4 chains, each with iter = 8000; warmup = 4000; thin = 1;
## total post-warmup draws = 16000
##
## Regression Coefficients:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## ic50_substance_idBTRX_335140 -8.84 0.20 -9.20 -8.42 1.00 15027 8248
## ic50_substance_idBTRX_395750 -8.24 0.41 -8.93 -7.36 1.00 11072 5925
## ic50_substance_idJNJ -9.15 0.31 -9.77 -8.50 1.00 15946 10770
## ic50_substance_idPF -6.14 1.08 -7.69 -3.32 1.00 7646 5332
## hill_substance_idBTRX_335140 -1.47 0.59 -2.85 -0.57 1.00 14309 9824
## hill_substance_idBTRX_395750 -0.91 0.52 -2.28 -0.26 1.00 10745 7238
## hill_substance_idJNJ -1.01 0.51 -2.38 -0.41 1.00 14567 11520
## hill_substance_idPF -0.31 0.24 -0.92 -0.03 1.00 7908 5627
## bottom_substance_idBTRX_335140 -0.00 0.49 -0.96 0.95 1.00 17746 11293
## bottom_substance_idBTRX_395750 0.01 0.50 -0.97 0.99 1.00 18472 10902
## bottom_substance_idJNJ -0.01 0.49 -0.99 0.96 1.00 17703 11821
## bottom_substance_idPF 0.01 0.50 -0.97 0.99 1.00 16850 11426
## top_substance_idBTRX_335140 100.00 0.00 100.00 100.00 NA NA NA
## top_substance_idBTRX_395750 100.00 0.00 100.00 100.00 NA NA NA
## top_substance_idJNJ 100.00 0.00 100.00 100.00 NA NA NA
## top_substance_idPF 100.00 0.00 100.00 100.00 NA NA NA
##
## Further Distributional Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma 32.17 2.90 27.13 38.38 1.00 14788 11389
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Traceplot: The model ran without warning messages,
meaning there were no parameter value problems or MCMC conflicts. The
bulk and tail ESS indicate high resolution and stability. The R-hat for
each parameter equals 1.00 and the traceplot
shows the chains mixed well, indicating the chains converged.
kor_model |>
bayesplot::mcmc_trace()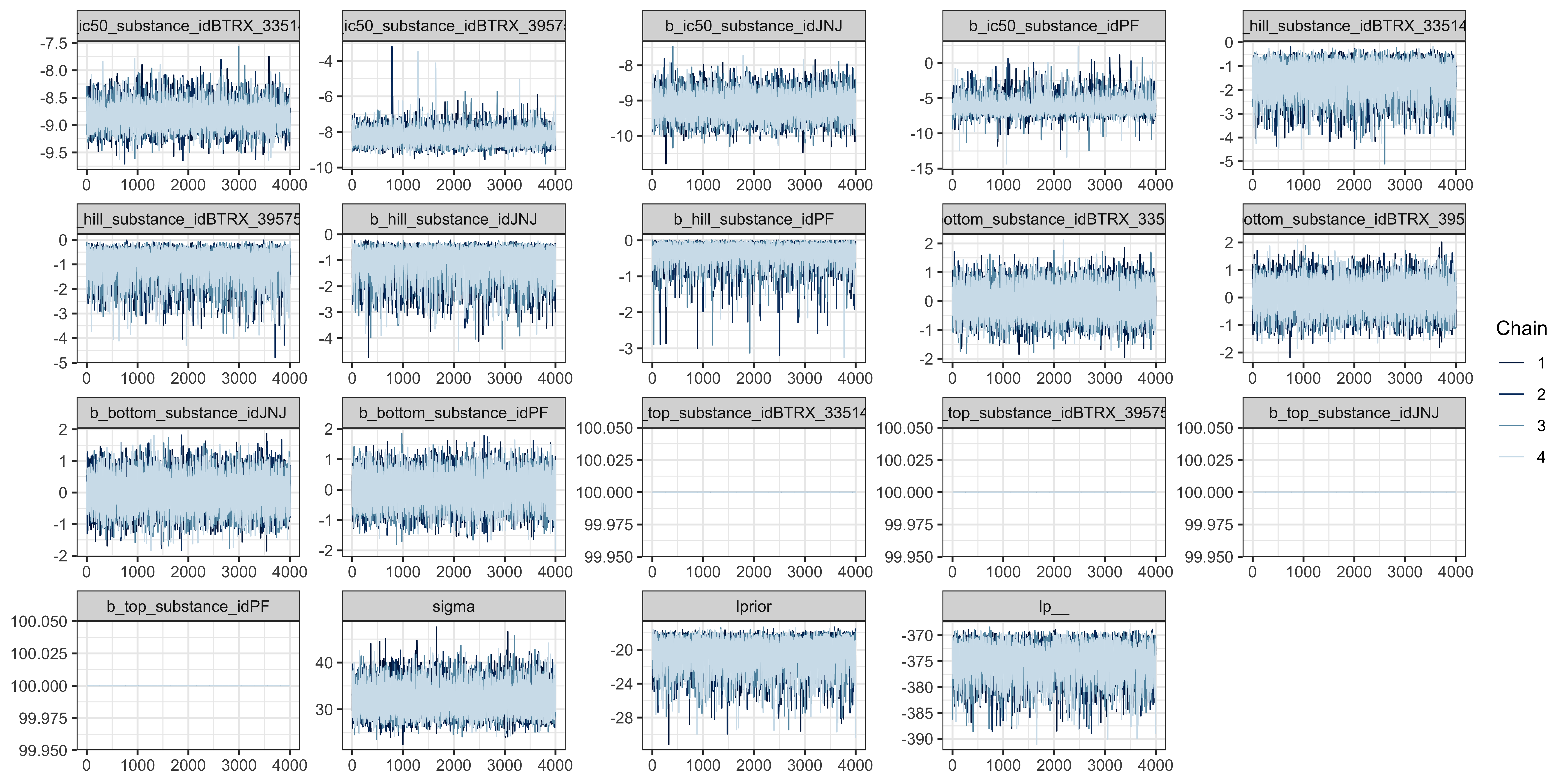
plot of chunk kor-model-traceplot
Compare prior and posterior marginal distributions: Displayed below is a plot for the prior and posterior distributions of the parameters (prior is pink and posterior is teal). This can be useful for comparing the density distribution of the prior and posterior produced by the model:
BayesPharma::plot_prior_posterior_densities(
model = kor_model,
title_label = "")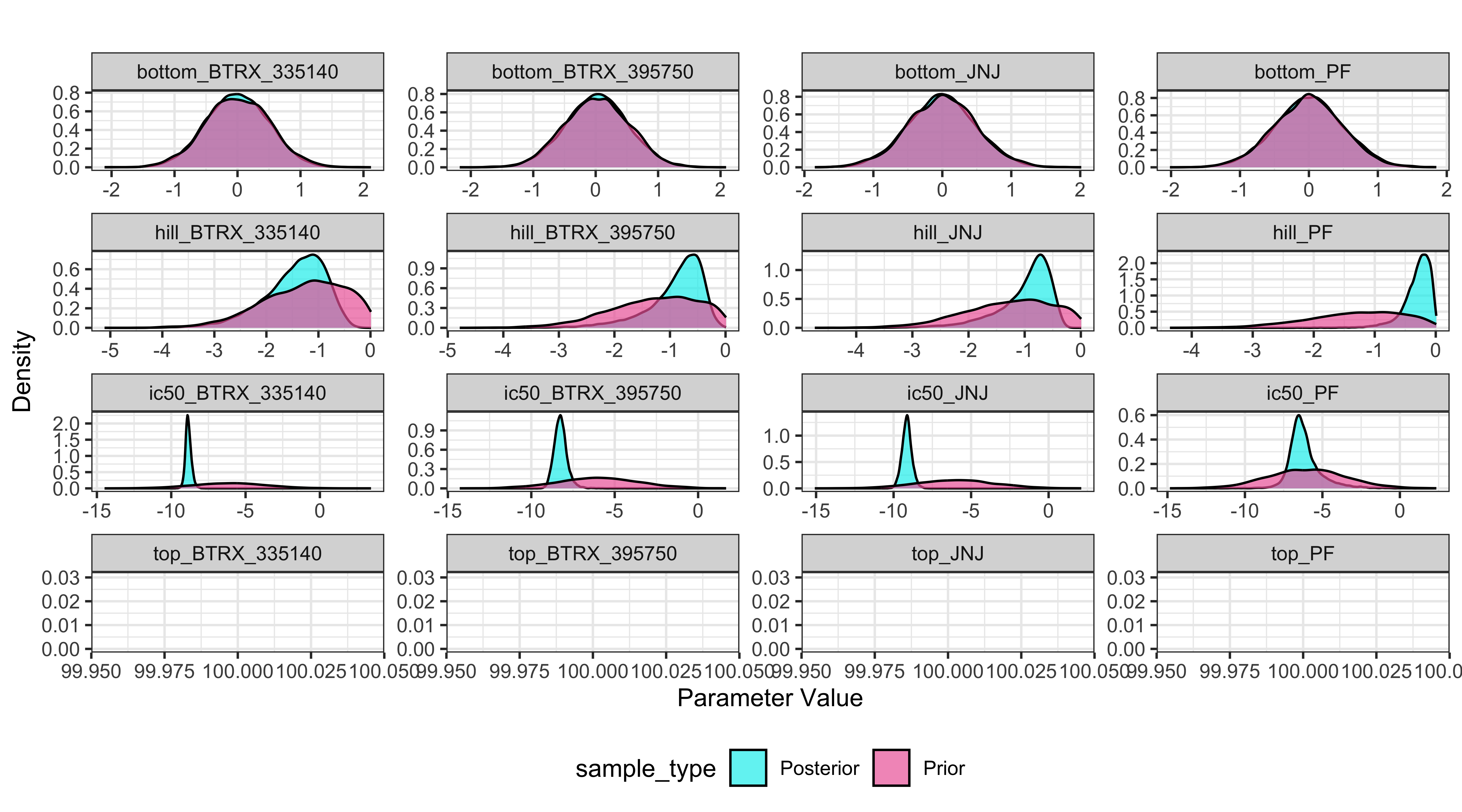
KOR antagonists model, compare prior and posterior distributions for each substance
Displayed below is a plot of the posterior distributions for each parameter with the confidence intervals and mean. This is a useful visual of the model results and can highlight the mode and high-density intervals:
BayesPharma::plot_posterior_density(
kor_model,
title_label = "")
## Error in `dplyr::filter()`:
## ℹ In argument: `!...`.
## Caused by error in `.data[[".variable"]]`:
## ! Column `.variable` not found in `.data`.Displayed below is a plot of a sample of 100 sigmoid dose-response curves from the posterior distribution (purple) and the median quantile intervals:
BayesPharma::plot_posterior_draws(
model = kor_model,
title = "")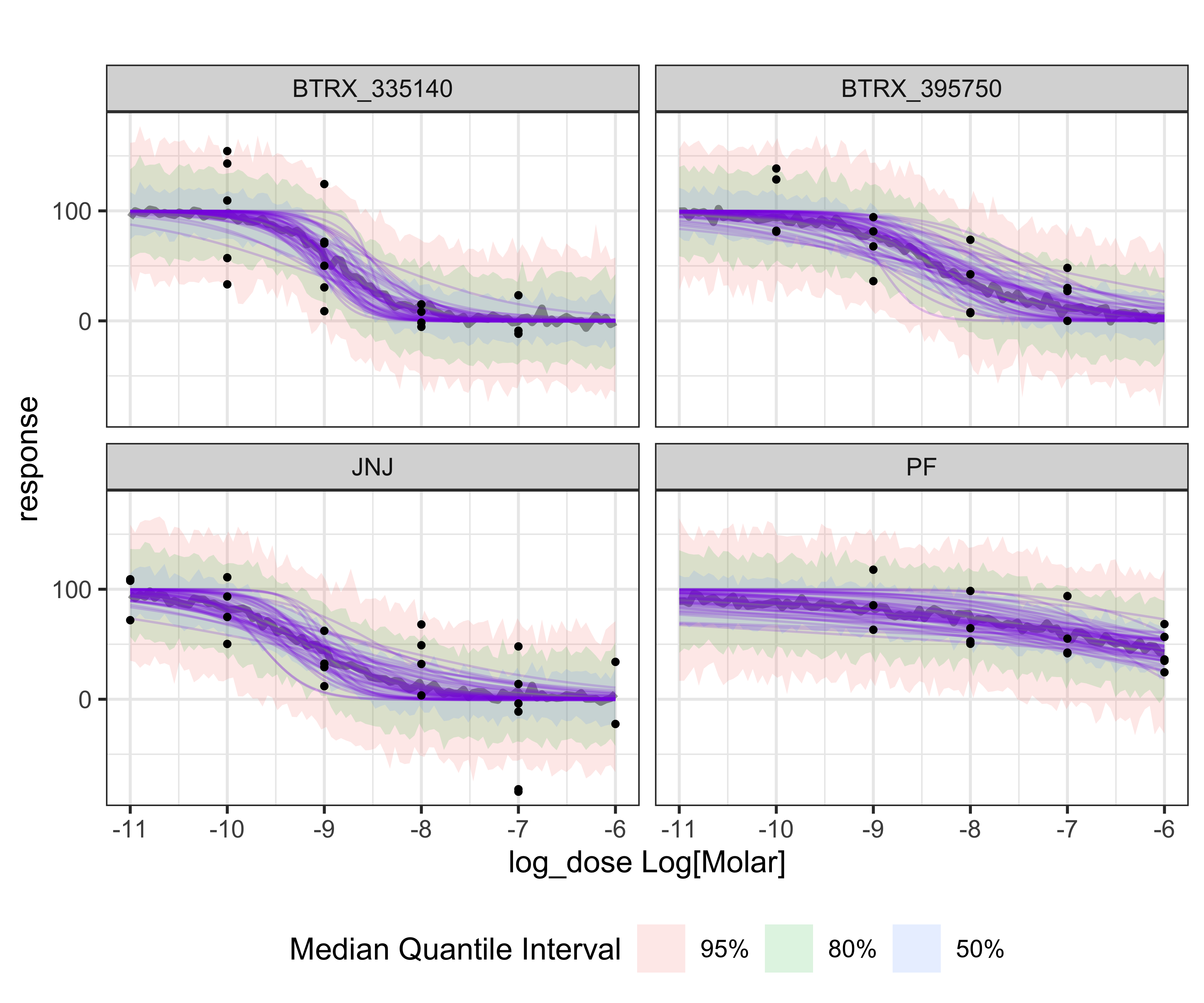
KOR antagonists, posterior draws
Comparing alternative models
To test the sensitivity of the analysis to the prior, we can re-fit the model with a more informative prior:
## prior class coef group resp dpar nlpar lb ub source
## normal(-8.5, 0.5) b ic50 <NA> <NA> user
## normal(-1, 0.5) b hill <NA> 0.01 user
## constant(100) b top <NA> <NA> user
## normal(10, 15) b bottom <NA> <NA> userRe-fitting the model with the kor_prior2 gives:
## Family: gaussian
## Links: mu = identity; sigma = identity
## Formula: response ~ sigmoid(ic50, hill, top, bottom, log_dose)
## ic50 ~ 0 + substance_id
## hill ~ 0 + substance_id
## top ~ 0 + substance_id
## bottom ~ 0 + substance_id
## Data: data (Number of observations: 73)
## Draws: 4 chains, each with iter = 8000; warmup = 4000; thin = 1;
## total post-warmup draws = 16000
##
## Regression Coefficients:
## Estimate Est.Error l-95% CI u-95% CI Rhat
## ic50_substance_idBTRX_335140 -8.82 0.21 -9.23 -8.37 1.00
## ic50_substance_idBTRX_395750 -8.58 0.31 -9.16 -7.94 1.00
## ic50_substance_idJNJ -8.95 0.31 -9.53 -8.32 1.00
## ic50_substance_idPF -8.18 0.45 -9.09 -7.30 1.00
## hill_substance_idBTRX_335140 -1.19 0.37 -1.99 -0.57 1.00
## hill_substance_idBTRX_395750 -1.06 0.39 -1.90 -0.42 1.00
## hill_substance_idJNJ -0.85 0.33 -1.65 -0.39 1.00
## hill_substance_idPF -0.72 0.45 -1.72 -0.07 1.00
## bottom_substance_idBTRX_335140 1.71 10.47 -19.21 21.94 1.00
## bottom_substance_idBTRX_395750 15.44 11.10 -7.30 36.02 1.00
## bottom_substance_idJNJ -2.77 9.82 -23.22 15.35 1.00
## bottom_substance_idPF 31.22 11.59 7.03 52.03 1.00
## top_substance_idBTRX_335140 100.00 0.00 100.00 100.00 NA
## top_substance_idBTRX_395750 100.00 0.00 100.00 100.00 NA
## top_substance_idJNJ 100.00 0.00 100.00 100.00 NA
## top_substance_idPF 100.00 0.00 100.00 100.00 NA
## Bulk_ESS Tail_ESS
## ic50_substance_idBTRX_335140 13087 10643
## ic50_substance_idBTRX_395750 12995 10960
## ic50_substance_idJNJ 13299 11776
## ic50_substance_idPF 13156 10947
## hill_substance_idBTRX_335140 14798 9835
## hill_substance_idBTRX_395750 13437 9765
## hill_substance_idJNJ 13283 11670
## hill_substance_idPF 8776 5539
## bottom_substance_idBTRX_335140 14068 12061
## bottom_substance_idBTRX_395750 12671 10835
## bottom_substance_idJNJ 12510 10615
## bottom_substance_idPF 10495 10156
## top_substance_idBTRX_335140 NA NA
## top_substance_idBTRX_395750 NA NA
## top_substance_idJNJ NA NA
## top_substance_idPF NA NA
##
## Further Distributional Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma 31.86 2.83 26.91 37.99 1.00 14470 11441
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Comparing the Two Models Using LOO-Comparison: One
way to evaluate the quality of a model is for each data-point, re-fit
the model with remaining points and evaluate the log probability of the
point in the posterior distribution. Taking the expectation across all
points gives the Expected Log Pointwise predictive Density (ELPD). Since
this is computationally challenging to re-fit the model for each point,
if the model fits the data reasonably well, then the ELPD can be
approximated using the Pareto smoothed importance sampling (PSIS). Using
the LOO package, Pareto k value for each data point is computed that
indicate how well that data point is fit by the model, where
k < 0.5 is good, 0.5 <= k < 0.7 is
OK, and 0.7 <= k is bad. Evaluating the model for the
KOR antagonists shows that the model fits the data well.
##
## Computed from 16000 by 73 log-likelihood matrix.
##
## Estimate SE
## elpd_loo -360.5 6.5
## p_loo 6.9 1.1
## looic 721.0 13.1
## ------
## MCSE of elpd_loo is 0.0.
## MCSE and ESS estimates assume MCMC draws (r_eff in [0.4, 1.4]).
##
## All Pareto k estimates are good (k < 0.7).
## See help('pareto-k-diagnostic') for details.Since ELPD is a global measure of model fit, it can be used to
compare models. Using loo_compare from the LOO package
returns the elpd_diff and se_diff for each
model relative the model with the lowest ELPD. The
kor_model2, the model with more informative prior, is the
preferred model, but not significantly.
## No problematic observations found. Returning the original 'loo' object.
## elpd_diff se_diff
## kor_model2 0.0 0.0
## kor_model -0.9 1.2Comparing against models fit with the drc
Package: Here we will analyze the KOR antagonist data using the
drc package and compare it to the results from the
BayesPharma analysis.
We will fix the top to 100 and fit the
ic50, hill, and bottom.
drc_models <- kor_antag |>
dplyr::group_by(substance_id) |>
dplyr::group_nest() |>
dplyr::mutate(
model = data |>
purrr::map(~drc::drm(
response ~ log_dose,
data = .x,
fct = drc::L.4(fixed = c(NA, NA, 100, NA),
names = c("hill", "bottom", "top", "ic50")))))
drc_models |>
dplyr::mutate(summary = purrr::map(model, broom::tidy, conf.int = TRUE)) |>
tidyr::unnest(summary) |>
dplyr::arrange(term, substance_id) |>
dplyr::select(-data, -model, -curve)
## # A tibble: 12 × 8
## substance_id term estimate std.error statistic p.value conf.low conf.high
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 BTRX_335140 bottom 1.31 19.4 0.0675 9.47e- 1 -40.0 42.6
## 2 BTRX_395750 bottom 29.5 9.40 3.14 7.85e- 3 9.20 49.8
## 3 JNJ bottom -18.1 26.7 -0.681 5.04e- 1 -73.7 37.4
## 4 PF bottom 39.4 30.8 1.28 2.22e- 1 -27.0 106.
## 5 BTRX_335140 hill 4.06 9.20 0.441 6.65e- 1 -15.5 23.7
## 6 BTRX_395750 hill 9.82 164. 0.0600 9.53e- 1 -344. 364.
## 7 JNJ hill 1.17 0.580 2.02 5.69e- 2 -0.0378 2.38
## 8 PF hill 1.13 1.33 0.855 4.08e- 1 -1.73 4.00
## 9 BTRX_335140 ic50 -8.91 0.308 -28.9 1.42e-14 -9.57 -8.26
## 10 BTRX_395750 ic50 -8.97 0.505 -17.8 1.70e-10 -10.1 -7.88
## 11 JNJ ic50 -8.77 0.670 -13.1 2.89e-11 -10.2 -7.37
## 12 PF ic50 -7.96 1.27 -6.29 2.78e- 5 -10.7 -5.23Displayed below is the comparison of results from drc
and BayesPharma for each parameter of the dose-response
curve. Here we see that the Bayesian method provides a distribution
curve as evidence and has smaller confidence intervals than most of the
standard errors provided by the drc method.
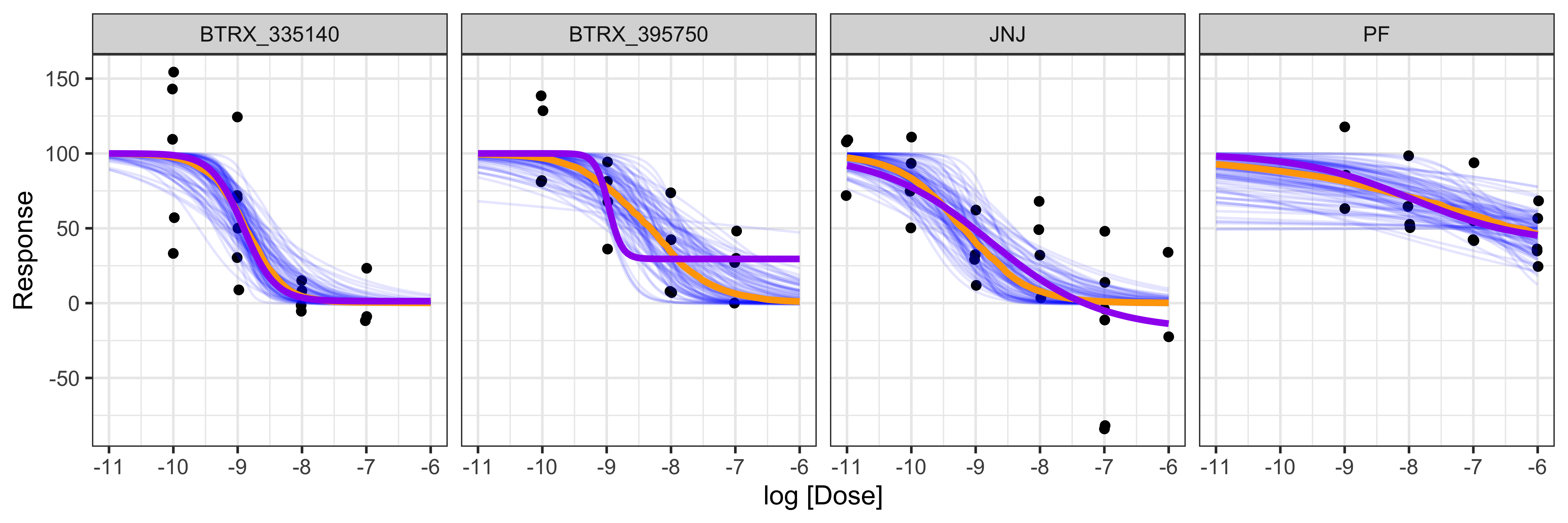
KOR antagonists conditional effects. The blue lines are samples from the
BayesPharma kor_model posterior distribution, the orange
line is the conditional mean, and the purple line is the conditional
mean for the drc model fit.